本文基于阿顾同学博客进行整理
原文链接https://blog.csdn.net/u010452388/article/details/81283998
文章内容我感觉是基于左神的课进行的整理,我曾经听过左神的课,也有笔记,倍感熟悉。
下面进入正题:
大根堆和小根堆
性质:每个结点的值都大于其左孩子和右孩子结点的值,称之为大根堆;每个结点的值都小于其左孩子和右孩子结点的值,称之为小根堆。如下图
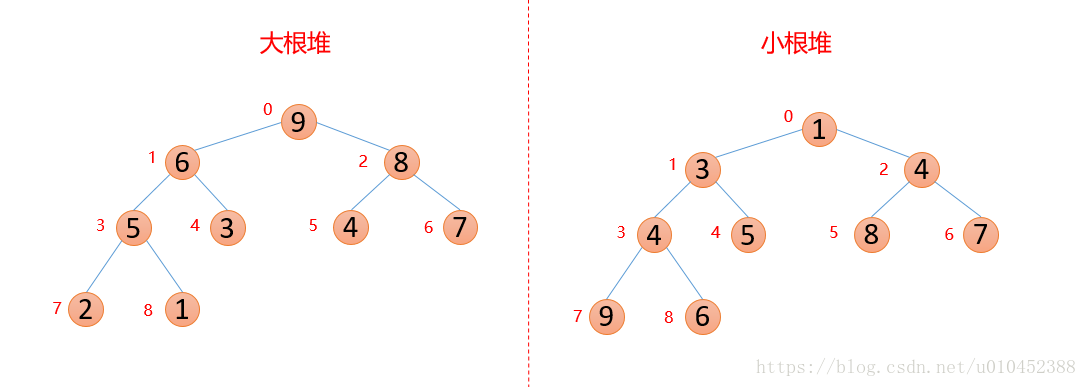
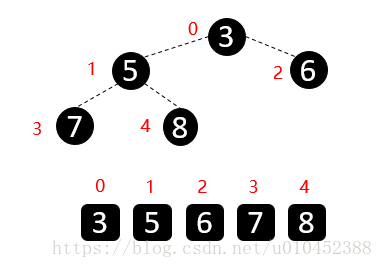
还有一个基本概念:查找数组中某个数的父结点和左右孩子结点,比如已知索引为i的数,那么
-
父结点索引:(i-1)/2(这里计算机中的除以2,省略掉小数)(python中用//即可)
-
左孩子索引:2*i+1
-
右孩子索引:2*i+2
上述公式是堆排序算法的核心。
所以上面两个数组可以脑补成堆结构,因为他们满足堆的定义性质(每个结点大于或者小于它的左孩子和右孩子):
大根堆:arr(i)>arr(2i+1) && arr(i)>arr(2i+2)
小根堆:arr(i)<arr(2i+1) && arr(i)<arr(2i+2)
堆排序基本步骤
基本思想:
-
首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
-
将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1(heap_size控制堆的大小,即heap_size - 1)
-
将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
1、构造堆
将无序数组构造成一个大根堆(升序用大根堆,降序就用小根堆)
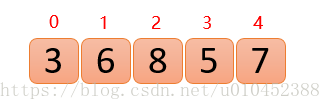
假设存在以下数组
主要思路:第一次保证0 ~ 0位置大根堆结构(废话),第二次保证0 ~ 1位置大根堆结构,第三次保证0 ~ 2位置大根堆结构…直到保证0 ~ n-1位置大根堆结构
方法:每次新插入的数据都与其父结点进行比较,如果插入的数比父结点大,则与父结点交换,否则一直向上交换,直到小于等于父结点,或者来到了顶端(寻找父节点采用索引,父结点索引:(i-1)/2)
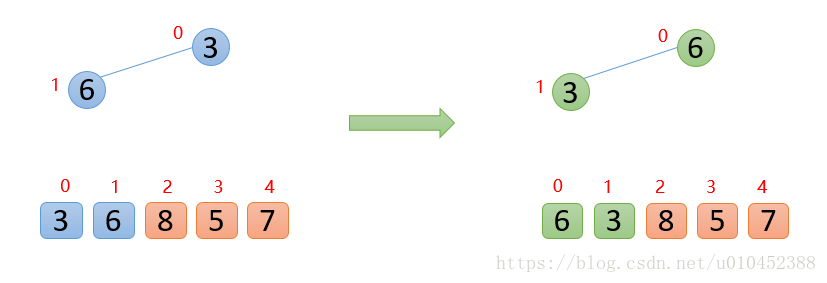
插入6的时候,6大于他的父结点3,即arr(1)>arr(0),则交换;此时,保证了0 ~ 1位置是大根堆结构,如下图:
(友情提示:待交换的数为蓝色,交换后的数为绿色)
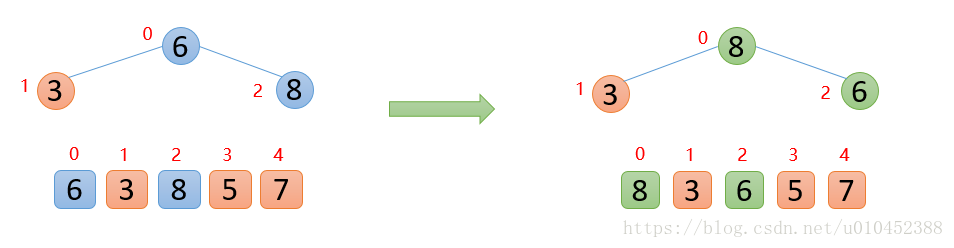
插入8的时候,8大于其父结点6,即arr(2)>arr(0),则交换;此时,保证了0~2位置是大根堆结构,如下图
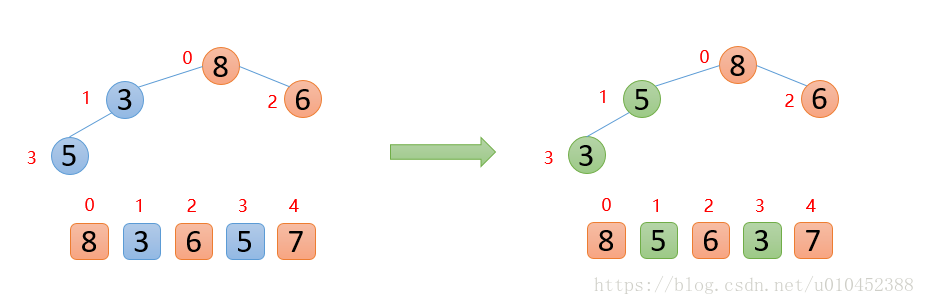
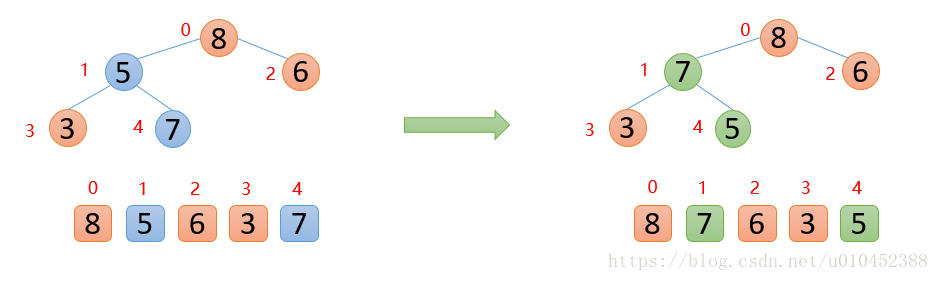
插入5的时候,5大于其父结点3,则交换,交换之后,5又发现比8小,所以不交换;此时,保证了0~3位置大根堆结构,如下图:
插入7的时候,7大于其父结点5,则交换,交换之后,7又发现比8小,所以不交换;此时整个数组已经是大根堆结构
2、固定最大值再构造堆
此时,我们已经得到一个大根堆,下面将顶端的数与最后一位数交换,然后将剩余的数再构造成一个大根堆
(友情提示:黑色的为固定好的数字,不再参与排序)
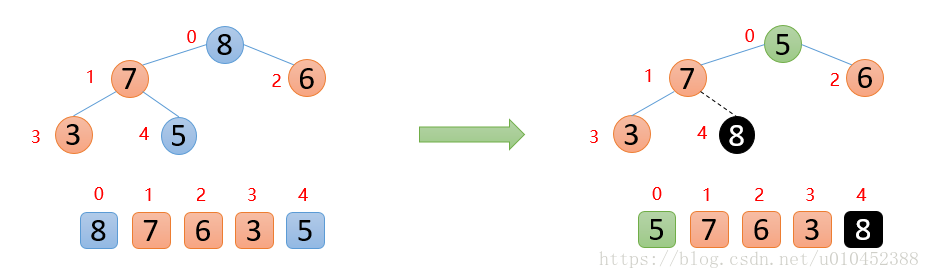
此时最大数8已经来到末尾,则固定不动,后面只需要对顶端的数据进行操作即可,拿顶端的数与其左右孩子较大的数进行比较,如果顶端的数大于其左右孩子较大的数,则停止,如果顶端的数小于其左右孩子较大的数,则交换,然后继续与下面的孩子进行比较
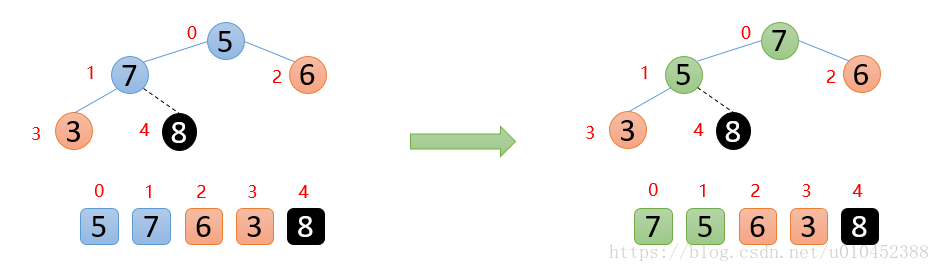
下图中,5的左右孩子中,左孩子7比右孩子6大,则5与7进行比较,发现5<7,则交换;交换后,发现5已经大于他的左孩子,说明剩余的数已经构成大根堆,后面就是重复固定最大值,然后构造大根堆
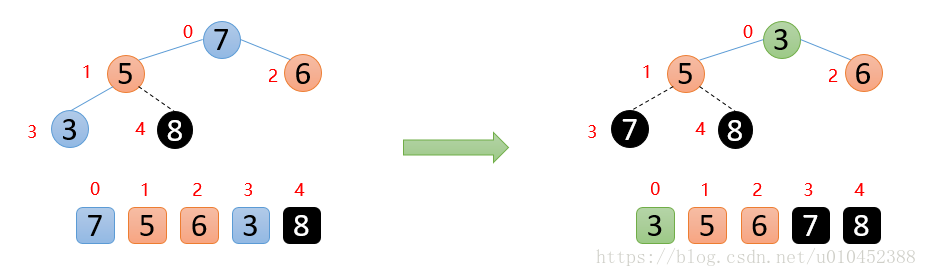
如下图:顶端数7与末尾数3进行交换,固定好7,
剩余的数开始构造大根堆 ,然后顶端数与末尾数交换,固定最大值再构造大根堆,重复执行上面的操作,最终会得到有序数组
总结
到这里,大家应该对堆排序都有了自己的见解,我们对上面的流程总结下:
-
首先将无需数组构造成一个大根堆(新插入的数据与其父结点比较)
-
固定一个最大值,将剩余的数重新构造成一个大根堆,重复这样的过程
代码
代码中主要两个方法:
-
将待排序数组构造成一个大根堆(元素上升)
-
固定一个最大值,将剩余的数再构造成一个大根堆(元素下降)
java代码如下:
//堆排序
public static void heapSort(int[] arr) {
//构造大根堆
heapInsert(arr);
int size = arr.length;
while (size > 1) {
//固定最大值
swap(arr, 0, size - 1);
size--;
//构造大根堆
heapify(arr, 0, size);
}
}
//构造大根堆(通过新插入的数上升)
public static void heapInsert(int[] arr) {
for (int i = 0; i < arr.length; i++) {
//当前插入的索引
int currentIndex = i;
//父结点索引
int fatherIndex = (currentIndex - 1) / 2;
//如果当前插入的值大于其父结点的值,则交换值,并且将索引指向父结点
//然后继续和上面的父结点值比较,直到不大于父结点,则退出循环
while (arr[currentIndex] > arr[fatherIndex]) {
//交换当前结点与父结点的值
swap(arr, currentIndex, fatherIndex);
//将当前索引指向父索引
currentIndex = fatherIndex;
//重新计算当前索引的父索引
fatherIndex = (currentIndex - 1) / 2;
}
}
}
//将剩余的数构造成大根堆(通过顶端的数下降)
public static void heapify(int[] arr, int index, int size) {
int left = 2 * index + 1;
int right = 2 * index + 2;
while (left < size) {
int largestIndex;
//判断孩子中较大的值的索引(要确保右孩子在size范围之内)
if (arr[left] < arr[right] && right < size) {
largestIndex = right;
} else {
largestIndex = left;
}
//比较父结点的值与孩子中较大的值,并确定最大值的索引
if (arr[index] > arr[largestIndex]) {
largestIndex = index;
}
//如果父结点索引是最大值的索引,那已经是大根堆了,则退出循环
if (index == largestIndex) {
break;
}
//父结点不是最大值,与孩子中较大的值交换
swap(arr, largestIndex, index);
//将索引指向孩子中较大的值的索引
index = largestIndex;
//重新计算交换之后的孩子的索引
left = 2 * index + 1;
right = 2 * index + 2;
}
}
//交换数组中两个元素的值
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
C++ 代码如下: (其实java的代码已经写的很去语言化了,这部分就是把细微的差异变一下,这里直接使用C++ std中的swap函数
void heapSort(vector<int>& arr) {
//构造大根堆
heapInsert(arr);
int size = arr.size();
while (size > 1) {
swap(arr[0], arr[size - 1]);
size--;
heapify(arr,0,size);
}
}
void heapInsert(vector <int>& arr){
int size = arr.size();
for (int i = 0;i < size; i++){
int currentindex = i;
int fatherindex = (currentindex - 1)/2;
while (arr[currentindex] > arr[fatherindex]){
swap(arr[currentindex], arr[fatherindex]);
currentindex = fatherindex;
fatherindex = (currentindex - 1)/2;
}
}
}
void heapify (vector <int>& arr, int index, int size){
int left = 2 * index + 1;
int right = 2 * index + 2;
while (left < size){
int largestindex;
if (arr[left] < arr[right] && right < size){
largestindex = right;
}
else{
largestindex = left;
}
if (arr[index] > arr[largestindex]) {
largestindex = index;
}
if (index == largestindex){
break;
}
swap(arr[largestindex], arr[index]);
index = largestindex;
left = 2 * index + 1;
right = 2 * index + 2;
}
}