归并排序

本文基于阿顾同学博客进行整理

原文链接https://blog.csdn.net/u010452388/article/details/81008727

原文链接https://blog.csdn.net/u010452388/article/details/81170368

图解流程

归并排序即采用二分法不断分解，分解到单个数的时候开始合并，最终合并为一个有序数组。

分解原理：每次找到数组中点（L + （R - L）»2）（这样有两个优点1、防溢出 2、速度快），将当前数组划分为两个数组，递归划分最终分解成一个数。

合并原理：归并的每一次合并都是将两个有序组合并为一个有序组，合并好后的有序组，再和另外的有序组继续合并，最终可以得到一个完整的有序数组

合并过程

整体流程如下：

细节流程：

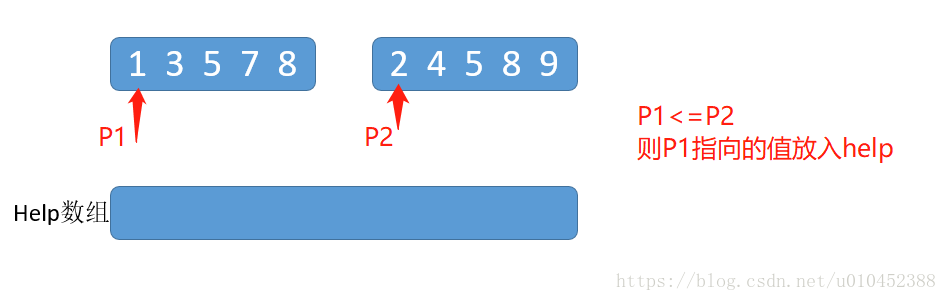
第一步：

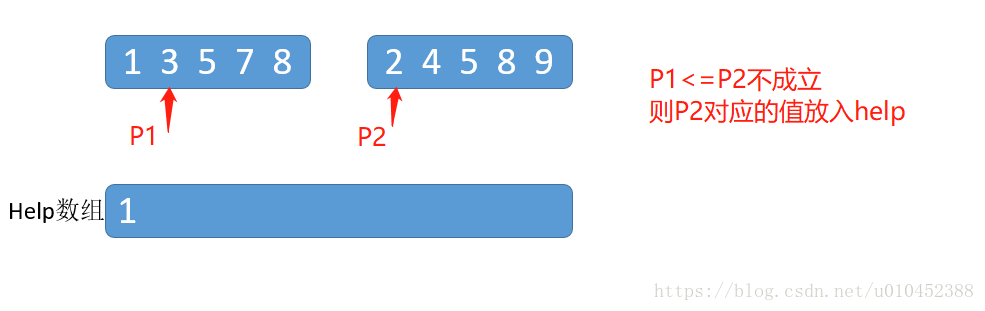
第二步：

第三步:

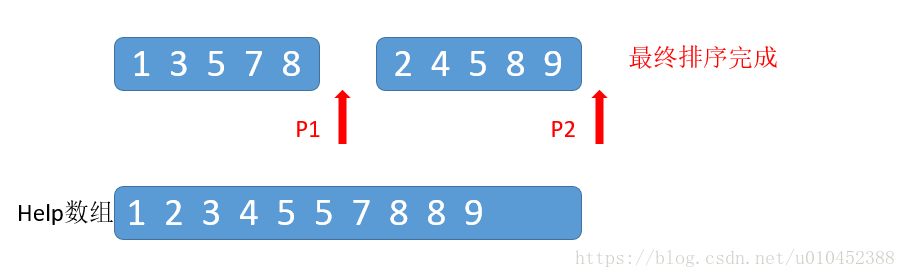
递归上述步骤，最终排序成功：

归并排序代码

java代码

public static void mergeSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        mergeSort(arr, 0, arr.length - 1);
    }

    public static void mergeSort(int[] arr, int L, int R) {
        if (L == R) {
            return;
        }
        int mid = (L + R) / 2;
        //将数组左侧全部排成有序
        mergeSort(arr, L, mid);//T(N/2)
        //将数组右侧全部排成有序
        mergeSort(arr, mid + 1, R);//T(N/2)
        merge(arr, L, mid, R);//O(N):因为N个数的话，需要依次扫过去
    }

    private static void merge(int[] arr, int L, int mid, int R) {
        //开辟一个临时数组，用来存放归并过程中的排好序的元素
        int[] help = new int[R - L + 1];
        //临时数组的索引
        int i = 0;
        int p1 = L;
        int p2 = mid + 1;
        while (p1 <= mid && p2 <= R) {
            if (arr[p1] <= arr[p2]) {
                help[i] = arr[p1];
                i++;
                p1++;
            } else {
                help[i] = arr[p2];
                i++;
                p2++;
            }
        }
        while (p1 <= mid) {
            help[i] = arr[p1];
            i++;
            p1++;
        }
        //上面的while循环和下面的while循环只会执行一个
        while (p2 <= R) {
            help[i] = arr[p2];
            i++;
            p2++;
        }
        for (int j = 0; j < help.length; j++) {
            // 这里要用arr[L+j]接受，因为每次进来归并排序的数组起始索引是L，长度是help的长度
            arr[L + j] = help[j];
        }
    }

Master公式

Master公式用于求递归问题的时间复杂度（其中堆排序的时间复杂度是用Master公式计算的数学期望）

T(N) = a * T(N/b) + O(N^d) 1) 如果log(b,a) > d –> 复杂度为O(N^log(b,a)) 2) 如果log(b,a) = d –> 复杂度为O(N^d * logN) 3) 如果log(b,a) < d –> 复杂度为O(N^d)

时间复杂度和额外空间复杂度

时间复杂度：

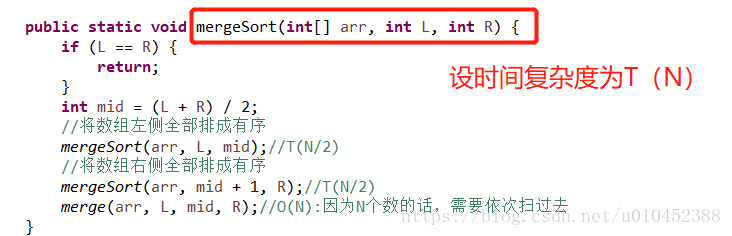
我们设mergeSort的时间复杂度为T(N)
从宏观上看，他分别调用了两次自己的函数mergeSort和一次merge,那么T(N)等于两次mergeSort的时间复杂度和一次merge的时间复杂度
调用自己的函数的时候，函数个数为N/2，则T(N)=2 * T(N/2)+一次merge的时间复杂度
根据上面的流程分析merge总共扫描了N个数，执行了N次，所以时间复杂度为O(N)
所以T(N)=2 * (N/2)+O(N)
根据Master公式，此时a=2,b=2,d=1,满足log(b,a) = d
所以归并排序时间复杂度为：O(N^d * logN)=O(N * logN)

额外空间复杂度：

因为我们每次执行merge的时候，都需要创建一个help数组，而这个help最大是N个数，需要N个空间，所以额外空间复杂度为O(N)，且merge过程不改变原来此，所以归并排序是稳定排序

解决小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。例子： [1,3,4,2,5] 1左边比1小的数，没有； 3左边比3小的数，1； 4左边比4小的数，1、3； 2左边比2小的数，1； 5左边比5小的数，1、3、4、2；所以小和为1+1+3+1+1+3+4+2=16

笨办法:

循环遍历每个数的左边的数与当前数进行比较，如果比当前数小，则累加起来，第一次遍历1次，第二次遍历2次，第n次遍历n次，是一个等差数列，但是时间复杂度为O(N^2)

代码

    public static int smallSum(int[] arr) {
        //声明累加变量
        int res=0;
        for (int i = 1; i < arr.length; i++) {
            //遍历索引小于i的元素，并进行判断
            for (int j = 0; j < i; j++) {
                if(arr[j]<arr[i]){
                    res+=arr[j];
                }
            }
        }
        return res;
    }

小和归并计算原理

这里主要就是利用合并的过程中，两个有序组都是有序的进行判断累加，我们以上图的数据为3,5组和数据为8,9组合并的过程为例，来计算累加的结果

从上面的图可以看出，如果p1索引的值小于p2索引的值，那么这一次排序的过程可以计算右侧数组比3大的数有2个（因为每一组都是有序的），然后索引p1向右移动

从上面的图可以看出，p1索引的值小于p2索引的值，那么这一次排序过程可以计算出右边比5大的数有2个

总结：上面两个有序组合并为一个有序组时，累加的小和的值为： 32+52=16

代码

    public static int smallSum(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;
        }
        return  mergeSort(arr,0,arr.length-1);
    }
 
    public static int mergeSort(int[] arr, int L, int R) {
        if (L == R) {
            return 0;
        }
        int mid = (L + R) >>>1;//这里是防止数据溢出
        return mergeSort(arr, L, mid) + mergeSort(arr, mid + 1, R) + merge(arr, L, mid, R);
    }
    //合并的过程
    public static int merge(int[] arr, int L, int mid, int R) {
        //准备一个临时数组，长度和传进来的arr一样
        int[] temp = new int[R - L + 1];
        int p1 = L;
        int p2 = mid + 1;
        //临时数组temp的索引起始变量
        int i = 0;
        //小和结果的变量
        int result = 0;
        //合并数组的循环，并计算小和
        while (p1 <= mid && p2 <= R) {
            if (arr[p1] < arr[p2]) {
                //计算小和的累加结果，(R-p2+1)为比数arr[p1]大的数量
                result += (R - p2 + 1) * arr[p1];
                temp[i] = arr[p1];
                p1++;
                i++;
            } else {
                temp[i] = arr[p2];
                p2++;
                i++;
            }
        }
        while (p1 <= mid) {
            temp[i] = arr[p1];
            i++;
            p1++;
        }
        while (p2 <= R) {
            temp[i] = arr[p2];
            i++;
            p2++;
        }
        //这里是将临时数组temp的元素重新赋值给传入进来的arr
        for (int j = 0; j < temp.length; j++) {
            arr[L + j] = temp[j];
        }
        return result;
    }

O(N * logN)时间复杂度